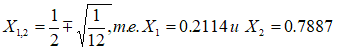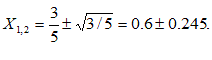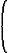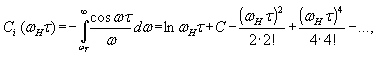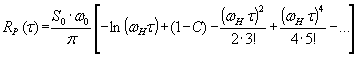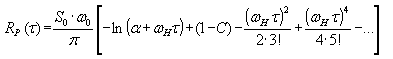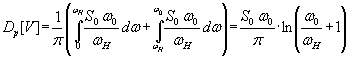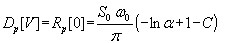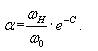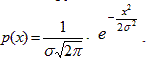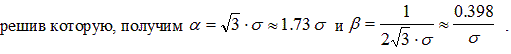Would you like to make this site your homepage? It's fast and easy...
Yes, Please make this my home page!
|
Сергей
Сибейкин.
МОЁ НАУЧНОЕ НАСЛЕДИЕ |
| |
|
Abstract=Основные положения. Исследуются измерения с операцией интегрирования. Последняя позволяет определять интеграл от
измериемой величины x(t) (т.е. входного сигнала датчика)(например, скорость V(t), когда датчик измеряет ускорение), либо
среднее значение x(t) (напряжение в вольтметре). Повышение точности измерения при наличии существенной погрешности линейности
(в том числе при использовании нелинейного датчика) можно решить применением ступенчатого опорного сигнала Xr,
аппроксимирующего ожидаемую измеряемую величину x(t).
1. Таким образом, процесс измерения разделяется на несколько этапов:
а) Предварительное измерение (или теоретические расчёты) для нахождения параметров ожидаемого измеряемого сигнала.
б) калибровка датчика в соответствии с результатами предыдущего пункта.
в) Измерение реального сигнала.
2. Измеряемый x(t) и опорный Xr сигналы рассматриваются как случайные, что позволяет использовать аппарат теории
вероятности и получить следующие важные выводы:
3. Для минимизации погрешности измерения моменты Mi опорного сигнала Xr должны быть равны соответствующим
моментам измеряемой величины x(t), где i - порядок момента.
4. Возможны три метода определения параметров опорного сигнала:
а) Вычисляются значения и продолжительности ступеней опорного сигнала - раздел 4.4.
б) Модифицирование предыдущего метода - заранее учитывается аддитивная погрешность, что позволяет повысить точность корркции
нелинейности - раздел 4.4.
Недостатком обоих методов является то, что для каждого измерения требуется проводить калибровку, чтобы выбрать значения ступеней
опорного сигнала, требуемый при ожидаемом входном сигнале. Не всегда возможно и обеспечить требуемые значения ступеней
опорного сигнала. Например, при измерении ускорения для калибровки мы не имеем значений больше
±g, а при измерении нередко ускорение достигает нескольких g.
в) Задаются значения и вычисляются продолжительности ступеней опорного сигнала - раздел 4.6. При этом самих ступеней
требуется в два раза больше, чем в обоих предыдущих методах. Достоинством этого метода является то, что выбранных заранее
значений опорного сигнала достаточно при любом входном сигнале. Этот метод наиболее удобен в реализации.
1
f = ¾¾¾
¾
s Ö
2p
ЧАСТЬ 1. ИНВАРИАНТНОСТЬ В ИЗМЕРЕНИИ и КОРРЕКЦИЯ НЕЛИНЕЙНОСТИ
ВВЕДЕНИЕ
Инвариантность - это неизменность (http://www.znanie-sila.ru/people/issue_84.html). В данном случае это означает, что результат
измерения остаётся неизменным несмотря на любые значения погрешности.
Моим научным руководителем при написании диссертации был Куликов Сергей Васильевич. У него же я работал в лаборатории. Нелёгкий
он был человек, но всё же научная работа, хоть и со скрипом, но продвигалась, и в конце концов кое-чего удалось добиться, а
окончательные результатыя получил уже после его смерти и моей эмиграции в США.
Источником работы послужила одна научная задача. Требовалось рассмотреть возможность применения для инерциальной навигации
пьезо-электрического акселерометра.
В нём пьезо-элемент, являющийся частью колебательного контура, находится под гнётом инерционной массы. Давление на
пьезо-элемент и, следовательно, его собственная частота, зависят от ускорения. Обычно используют 2 пьезо-элемента, включённые по
дифференциальной схеме. Тем не менее, погрешность линейности такого прибора остаётся значительной.
В перспективе предполагалась разработка спидометра, определяющего скорость путём интегрирования выходного параметра
пьезо-акселерометра - частоты следования импульсов, пропорциональной ускорению. Это можно сделать на обычном счётчике импульсом.
1-м шагом в разработке стала более узкая задача - определение момента, когда скорость V(t) достигнет некоего заданного значения
Vr. У немцев такая задача стояла уже при разработке ФАУ-2 - было необходимо отключить двигатель ракеты, когда её скорость
достигнет значения Vr. При этом применялся электролитический интегратор. Я в советской армии служил на ракете 8К63,
в к-рой применялась такая же технология.
ИНЕРЦИАЛЬНАЯ НАВИГАЦИЯ
Это - метод навигации (определения координат и параметров движения различных объектов - судов, самолётов, ракет и др.) и управления
их движением, основанный на свойствах инерции тел, являющийся автономным, т.е. не требующим наличия внешних ориентиров или
поступающих извне сигналов.
Сущность инерциальной навигации состоит в определении ускорения объекта и его угловых скоростей с помощью установленных на
движущемся объекте приборов и устройств, а по этим данным - местоположения (координат) этого объекта, его курса, скорости,
пройденного пути и др., а также в определении параметров, необходимых для стабилизации объекта и автоматического управления его
движением. Это осуществляется с помощью:
- датчиков линейного ускорения (акселерометров);
- гироскопических устройств, воспроизводящих на объекте систему отсчёта (например, с помощью гиростабилизированной платформы) и
позволяющих определять углы поворота и наклона объекта, используемые для его стабилизации и управления движением;
- вычислительных устройств (ЭВМ), которые по ускорениям (путём их интегрирования) находят скорость объекта, его координаты и
др. параметры движения.
Преимущества методов инерциальной навигации состоят в автономности, помехозащищённости и возможности полной автоматизации всех
процессов навигации. Благодаря этому методы инерциальной навигации получают всё более широкое применени при решении проблем
навигации надводных судов, подводных лодок, самолётов, космических аппаратов и других движущихся объектов.
1. ПОСТАНОВКА ЗАДАЧИ
Процесс интегрирования - важная часть точного измерения. Измеряемая величина воздействует на вход датчика, являясь его входным
сигналом x(t). Интегрированию подвергается выходной сигнал датчика y(t), связанный с его входным сигналом x(t) функцией
преобразования датчика. Результат интегрирования W(t) величины y(t) сравнивается с результатом интегрирования Wr
опорного сигнала Xr.
При измерении среднего значения входного сигнала x(t) сначала интегрируется x(t), а затем опорный сигнал Xr. Иногда же
нас интересует интеграл от входного сигнала x(t). Например, достижение скорости V(t) заданного значения Vr, если
входной сигнал x(t) - ускорение. В этом случае сначала интегрируется опорный Xr, а затем входной x(t) сигналы.
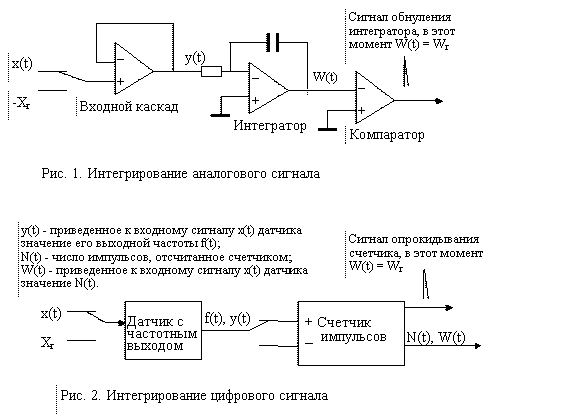
Выходной сигнал y(t) может быть аналоговый или цифровой, например, в виде частоты следования импульсов. Соответственно, интегратор
должен быть либо аналоговый (например, в вольтметре двухтактного интегрирования, рис. 1), либо цифровой, в виде счётчика
импульсов (рис. 2).
Для калибровки нелинейного датчика необходимо использование нескольких калибровочных сигналов X1, X2, . . .
Xi. Соответственно, при измерении нелинейным датчиком мы используем ступенчатый опорный сигнал Xr с
значениями ступеней X1, X2, . . . Xi, и их продолжительностями X1, X2,
. . . Xi.
pr(x) = b, если -a < x < a;
pr(x) = 0, если x < -a или x > a.
2. ИЗМЕРЕНИЕ
2.1. Мы интегрируем выходной сигнал Y датчика. Результат для опорного сигнала
для входного сигнала
Обозначим через T момент времени t, когда величина W(t) достигает значения Wr: W(T) = Wr . Величины W(T) и
Wr являются соответствнно показаниями величин
| T | Tr | |
| V(T) = | òx(t)×dt и Vr = | òXr×dt | | (2) |
| 0 | 0 | | |
Из-за погрешностей датчика значения V(T) и Vr отличаются на значение погрешности измерения DT = V(T) - Vr .
2.2. Рассмотрим погрешность измерения DV.
Из-за погрешностей датчика значения Vr и V(t) отличаются от значений Wr и W(t):
DVr = Wr; DV(t) = W(t) -
V(t).
Так как при t = T, W(T) = Wr, то погрешность измерения DV = V(T) - Vr = DVr -DV(T) .
Величина DV = 0, если DV(T) = DVr . Следовательно,
погрешность измерения DV минимальна, если после интегрирования погрешности от входного
x(t) и опорного Xr сигналов равны.
ПОГРЕШНОСТЬ ИЗМЕРЕНИЯ И ЕЁ МИНИМИЗАЦИЯ
3.1. Характеристики входного и опорного сигналов и датчика:
a) Мы рассматриваем входной x(t) и опорный Xr сигналы как случайные величины. Основной характеристикой случайной величины X является её плотность вероятности p(x)
Она имеет два свойства [5]:
| - плотность вероятности неотрицательна: p(x) ³ 0; | | | (3) |
| | ¥ |
| - интеграл от плотности вероятности равен единице: | ò p(x)×dx = 1 | | (4) |
| | -¥ |
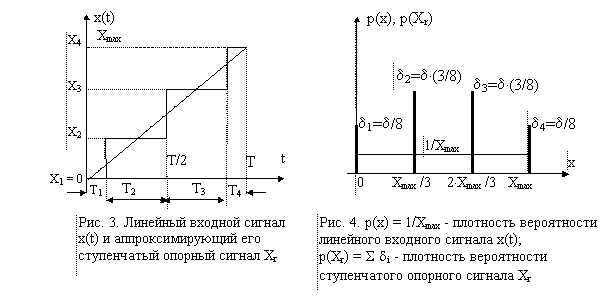
Для линейного входного сигнала x(t), изображенного на рис.4, плотность вероятности p(x) имеет равномерное распределение. Из выражения (4) можно найти p(x) = 1/Xmax.
Пусть опорный сигнал Xr имеет n ступеней. Тогда его плотность вероятности p(Xr) есть композиция функций di, пропорциональных дельта-функции d [6]:
где d = (Ti/T)d
Плотности вероятности p(x) и p(Xr) изображены на рис. 4.
Для описания случайной величины X используются также её моменты. Начальный момент Mi i-го порядка для случайной величины X описывается следующей формулой:
Можно также определить момент Mi как математическое ожиданип переменной x(t) в степени i:
| T | |
| Mi = (1/T) | òxi(t)dt | | (7) |
| 0 |
б) Основной характеристикой датчика является передаточная функция y = f(x), связывающая входной X и входной Y сигналы датчика. Мы будем описывать передаточную функцию рядом Маклорена:
| y = a0 + (1+ a1)×x + a2×x2 + a3×x3 + . . . | | (8) | | |
Здесь a0 есть аддитивная погрешность, a1 - погрешность крутизны датчика, a2, a3 . . . описывают погрешность линейности.
Идеальный датчик имеет передаточную функцию y = x.
3.2. Алгоритм для оптимального опорного сигнала
Минимизируем погрешность измерения. Для этого раскроем и приравняем выражения для величин W(T) и Wr.
Раскроем выражения (1) и (2) с учётом выражений (7) и (8). Тогда
| W(T) = T×(M1 + a1×M1 + a2×M2 + a3×M3 + . . .) | | (9) |
| Wr =T1×X1 +T2×X2 +T3×X3 + . . . + a0×(T1 +T2 +T3 + . . . ) + a1×(T1×X1 +T2×X2 +T3×X3 + . . . ) + a2×(T1×X12 +T2×X22 +T3×X32 + . . . ) + . . . |
(10) |
Учтём, что T×M1 - это величина V(T), T1×X1 +T2×X2 +T3×X3 + . . . - это Vr. Тогда, приравняв выражения (9) и (10), мы найдём погрешность измерения DV = V(T) - Vr:
| DV = a0×(T1 +T2 +T3 + . . . + Tn - T) + a1×(T1×X1 +T2×X2 +T3×X3 + . . . + Tn×Xn - T×M1) + a2×(T1×X12 +T2×X22 +T3×X32 + . . . Tn×Xn2 -
T×M2) + . . . + an-1×(T1×X1i-1 +T2×X2n-1 +T3×X3n-1 + . . . Tn×Xin-1 - T×Mi-1) + . . . | | (11) |
Погрешность DV равна нулю при любой функции преобразования датчика порядка n-1, если выражения, заключённые в скобках в правой части формулы (11) будут равны нулю. Ограничившись первыми "n" членами выражения (11), получим следующие условия для значения погрешности DV = 0:
T = T1 + T2 + . . . + Tn;
T×M1 = T1×X1 + T2×Xn + . . . + Tn×Xn;
T×M2 = T1×X12 + T2×Xn2 + . . . + Tn×Xn2;
T×M3 = T1×X13 + T2×Xn3 + . . . + Tn×Xn3;
| 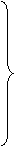 | (12) |
| . | . | . | . | . | . |
| T×Mn = T1×X1n + T2×Xnn + . . . + Tn×Xnn.
|
Так как T1 + T2 + T4 + . . . + Tn = Tr, то умножив и разделив правую часть уравнений (12) на величину T, мы можем записать систему уравнений (12) в более компактном виде:
T×Mi = Tr×Mr,i, i = 0, 1, 2. . . . n-1,
здесь Mr,i - момент i-го порядка опорного сигнала Xr, рассматривамого как случайная вличина; n - число ступеней опорного сигнала Xr. Напомним, что начальный момент нулевого порядка всегда равен 1.
Следовательно, погрешность измерения минимальна, если продолжительности и моменты входного и опорного сигналов равны.
Ступенчатый опорный сигнал с "n" ступенями может уменьшить погрешность измерения DV для первых "n-1" членов функции пробразования (8) до нуля, если мы точно определим моменты Mi ожидаемого входного сигнала.
Следовательно, чтобы найти оптимальный опорный сигнал, мы должны решить задачу проблемы моментов, т.е. найти параметры ступенчитого опорного сигнала, имеющего моменты, равные моментам входного сигнала.
3.3 РЕАЛИЗАЦИЯ МЕТОДА ИНВАРИАНТНОСТИ ПРИ ВЫЧИСЛЕНИИ ЗНАЧЕНИЙ И ПРОДОЛЖИТЕЛЬНОСТИ СТУПЕНЕЙ ОПОРНОГО СИГНАЛА
Запишем первые четыре уравнения системы(12), ограничившись первыми двумя членами каждого уравнения. Мы получим:
T = T1 + T2;
T×M1 = T1×X1 + T2×X2;
T×M2 = T1×X12 + T2×X22;
T×M3 = T1×X13 + T2×X23.
| 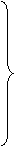 | (14) |
Эта система уравнений соответствует двух-ступенчатому опорному сигналу, причём нам надо найти продолжительность и величину каждой ступени.
Система уравнений (14) имет 4 неизвестных: T1, T2, X1, X2, |
X2 - |
M4 - M1×M2
__________ |
× X + |
M1×M4 - M22
___________ | |
= 0 | | (15) |
| M2 - M12 |
M2 - M12 | |
Из этого уравнения находим значения обоих ступеней опорного сигнала X1 и X1. Затем из любых 2-х уравнений системы (14) нетрудно найти продолжительности этих ступеней T1 и T1.
Для наглядности рассмотрим Численный пример 1.
Пусть величина Vr = 0.5; ожидаемый входной сигнал x(t) увеличивается линейно x(t) = t. Тогда T = 1 и моменты ожидаемого сигнала M1 = 1/2, M2 = 1/4, M4 = 1/4. Функцию преобразования датчика примем:
y = 1 + 2x + x2 + x4,
то есть все коэффициенты погршностей - аддитивной, мультипликативной и каждого члена погрешности линейности равны 1.
Решением уравнения (15) найдём значения ступеней опорного сигнала
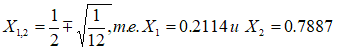
Затем находим продолжительности ступеней опорного сигнала T1 = T2 = 0.5.
От опорного сигнала в счётчик записана величина
Wr = T1×Y1 + T2×Y2 = T1×(1 + 2X1 + X12 + X14) + T2×(1 + 2X2 + X22 + X24) = 2.5833.
Показание интеграла входного сигнала при x(t) = t за время T = 1:
| T | 1 | | |
| W(t) = | òy(t)×dt = | ò(1 + 2t + t2 + t3)dt = 1 + 1+ 1/3 + 1/4 =2.5833 | | |
| 0 | 0 | | |
Таким образом, действительно, когда W(t) = Wr, время t = T и скорость V(t) = t2/2 достигнет заданного значения Vr = 0.5. Измерение произведено с высокой точностью несмотря на имющиеся погрешности.
Вот на этом и закончилась моя совместная работа с моим научным руководителем С.В.Куликовым, на этом матриале я защищал свою кандитатскую диссертацию. Дальнейшую работу, после смерти С.В.Куликова, проводил уже самостоятельно.
3.4. МОДИФИЦИРОВАННЫЙ МЕТОД РЕАЛИЗАЦИИ ИНВАРИАНТНОСТИ ПРИ ВЫЧИСЛЕНИИ ЗНАЧЕНИЙ И ПРОДОЛЖИТЕЛЬНОСТЕЙ СТУПЕНЕЙ ОПОРНОГО СИГНАЛА
Аддитивную погрешность нетрудно учесть заранее - ведь она не зависит от изменения входного сигнала. Если это сделать, то можно модифицировать систему уравнения (12). Отказавшись от 1-го уравнения системы, можно записать следующее уравнение более высокого порядка. Этим достигается компенсация влияния ещё одного члена полинома (8), описывающего погрешность датчика. Система уравнений (14) принимает следующий вид:
T×M1 = T1×X1 + T2×Xn + . . . + Tn×Xn;
T×M2 = T1×X12 + T2×Xn2 + . . . + Tn×Xn2;
T×M4 = T1×X14 + T2×Xn4 + . . . + Tn×Xn4;
| 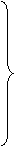 | (16) |
| . | . | . | . | . | . |
| T×Mn = T1×X1n + T2×Xnn + . . . + Tn×Xnn.
|
Эта система уравнений для двух-ступенчатого опорного сигнала выглядит:
T×M1 = T1×X1 + T2×X2;
T×M2 = T1×X12 + T2×X22;
T×M3 = T1×X13 + T2×X23.
T×M4 = T1×X14 + T2×X24.
|
 | (17) |
Решением этой системы тоже является уравнение 2-й степени, поскольку, к нашему удовольствию, члены 3-го порядка неизвестного X сократились. Это уравнение выглядит так:
X2 - |
M4×M1 - M4×M2
______________ |
× X + |
M42 - M4×M2
___________ | |
= 0 | | (18) |
| M22 - M4×M1 |
M22 - M4×M1 |
Для наглядности рассмотрим Численный пример 2.
Повторим численный пример1, только аддитивную погрешность примем равной нулю и, соответственно, добавим ещё один член для погрешности линейности:
y = 2x + x2 + x3 + x4.
Тогда из решения уравнения (18) найдём X1 и X2, и тогда из любых 2-х уравнений системы (17) найдём T1 и T2.
Уравнение (18) вида: x2 + px +q = 0. Для ожидаемого линейно возрастающего сигнала значения моментов: M1 = 1/2, M2 = 1/3, M3 = 1/4, M4 = 1/5. Соответственно находим p = 6/5, q = 3/10. Тогда
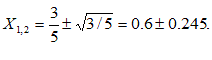
X1 = 0.3551 и X2 = 0.8449.
Следовательно, T1 = 0.5125 и T2 = 0.3764. Сумма T1×X1 + T2×X2 0.5000 получилась правильная, а вот T1+T2 = 0.8889. Это интересно, их сумма не совпадат с T. Впрочем, этого и следовало ожидать.
От опорного сигнала в счётчик записана величина
| T |
| Wr = | òYr×dt = T1×(2X1 + X12 + X13 + X14) + T2×(2X2 + X22 + X23 + X24) = 1.7833. |
| 0 |
Показание интеграла входного сигнала при x(t) = t за время T = 1:
| T | T |
| W(t) = | òy(t)×dt = | ò(2t + t2 + t3 + t4)dt = 1 + 1/3 + 1/4 + 1/5 = 1.7833. |
| 0 | 0 |
Как видим, как и в предыдущем случае, полная компенсация влияния погрешностей.
3.5. ОГРАНИЧЕНИЯ РАССМОТРЕННЫХ МЕТОДОВ И ИХ ПРЕОДОЛЕНИЕ
Поворотом пьзоакселерометра вокруг местной вертикали можно изменять значения ступеней опорного сигнала и получить любые нужные нам величины X1 и X2, но, конечно, в пределах ±g. Если требуется ступень опорного сигнала больше g, то реализация данного метода не работает.
Кроме того, далеко не всегда можно произвольно выбирать значения ступеней опорного сигнала. Обычно они заданы заранее. Например, для напряжения значения опорных сигналов задаются стабилитронами, и их просто невозможно варьировать, как требует рассмотренный метод.
Возникшие трудности можно обойти в ниже-приведённой реализации метода инвариантности, в к-ром для значния ступеней опорного сигнала могут быть низменными )) неизменными и в несколько раз меньше значения измеряемого сигнала.
3.6. РЕАЛИЗАЦИЯ МЕТОДА ИНВАРИАНТНОСИ ПРИ ЗАДАНИИ ЗНАЧЕНИЙ И ВЫЧИСЛЕНИИ ПРОДОЛЖИТЕЛЬНОСТЕЙ СТУПЕНЕЙ ОПОРНОГО СИГНАЛА.
Мы можем выбрать значения ступеней X1, X2 . . Xn опорного сигнала и найти требуемые продолжитльности T1, T2 . . Tn этих ступеней решением системы уравнений (12) через определители.
Для наглядности рассмотрим Численный пример 3.
Пусть, как и раньше, величина Vr = 0.5; ожидаемый входной сигнал x(t) увеличивается линейно x(t) = t. Функцию преобразования датчика примем y = x + x3, то есть датчик имеет только погрешность линейности, характеризуемую полиномом 3-й степени. В соответствии с системой уравнений (12) необходим опорный сигнал с 4-мя ступенями. При выбранной функции преобразования датчика вычисления будут наиболе просты и сводятся к решению би-квадратного уравнения, а система уравнений (12) примет следующий вид:
T = T1 + T2 + T3 + T4;
T×M1 = T1×X1 + T2×X2 + T3×X3 + T4×X4;
T×M2 = T1×X12 + T2×X22 + T3×X32 + T4×X42;
T×M3 = T1×X13 + T2×X23 + T3×X33 + T4×X43.
|
 |
Значения ступеней опорного сигнала примем равномерно распределёнными вдоль шкалы измерения: X1 = 0; X2 = 1/3; X3 = 2/3; X4 = 1. В соответствии с выражением (6), или (7), первый, второй и третий начальные моменты входного сигнала x(t): M1 = 1/2; M2 = 1/3; M3 = 1/4. Тогда решением системы уравнений через детерминанты получим:
T1 = T/8; T2 = 3× T/8; T1 = 3× T/8; T1 = T/8, и
| 4 | | 4 | |
| Wr = | S | Yi×Ti = | S | (Xi + Xi3)×Ti = 0×1/8+(1/3+1/27)×3/8+(2/3+4/27)×3/8+(1+1)×1/8=3/4 |
| i=1 | | i=1 | |
| t | t | t | |
| Величина W(t) = | òy(t)dt = | ò[x[(t) + x3(t)]dt = | ò(t + t3)dt = t2/2 + t4/4 | |
| 0 | 0 | 0 | |
Когда величина W(t) достигнет значения Wr, компаратором подаётся сигнал окончания измерения. В этот момент t = T, W(T) = Wr и T4/4 + T2/4 = 3/4. Корни этого би-квадратного уравнения следующие:
| | __ |
| T1,2 = ±1; T3,4 = ± | Ö | 3. |
Физический смысл имет только корень T1 = 1. При T = 1
| T | T | | |
| V(T) = | òx(t)dt = | òt×dt = 0.5 | | |
| 0 | 0 | | |
Следовательно V(T) = Vr, абсолютная DV = V(T) - Vr и относительная d(V) = DV/Vr погрешности измерения равны нулю.
Погрешность линейности датчика не повлияла на точность измерения.
Конечно, реальный входной сигнал в каждом конкретном измерении будет несколько отличаться от ожидаемого. Однако даже приблизительная оценка позволяет значительно повысить точность измерения.
Особенно высокую точность можно достигнуть, если в процессе измерения вычислять начальные моменты входного сигнала x(t) и по ним требуемые продолжительности Ti ступеней опорного сигнала Xi. Ведь в соответствии с выражением (2) нам нет нужды для вычисления величины Wr каждый раз проводить интегрировани опорного сигнала. Операцию интегрирования можно заменить операциями умножения и сложения, проводимых на вычислительном устройстве, ибо после калибровки мы знаем значения Yi для соответствующих ступеней опорного сигнала Xi.
Численный пример 4
Пусть реальный входной сигнал отличается от ожидаемого на 10%: x = 0.9×t. Тогда
| t | | | |
| W(t) = | ò(0.9×t + 0.729×t3)×dt = [0.9×t2/2] + [0.729×t4/4] | | | |
| 0 | | | |
Продолжая так же, как в Численном примере 1, найдём что T = 1.068, V(T) = 0.513 и относительная погрешность измерения
d(V) = DV/Vr = 2.6%.
Точно так же, при x = 0.99×t погрешность dV = 0.25%, при x = 0.999×t погрешность dV = 0.025%. Чем ближе реальный и ожидаемый входные сигнала, тем выше точность измерения.
Сравним эти результаты с классическим случаем одного опорного сигнала. Примем, что опорный сигнал находится в середине диапазона измерения Xr. Тогда время действия опорного сигнала Tr = Vr/Xr = 1, величина Wr = Yr×Tr + T = (Xr + Xr3)×Tr = 0.625. При x = t, решая, как и ранее, би-квадратное уравнение cо значением Wr = 0.625, получим: T = 0.933, V(T) = 0.4354, d(V) = DV/Vr = 12.5%. Как видим, метод инвариантности обеспечивает значительное повышние точности измерения.
3.7. Случай, когда опорный сигнал покрывает только часть входного сигнала
Пока мы находимся в рамках классической теории вероятности. Но это только потому, что наш опорный сигнал покрывает весь входной сигнал, что не всегда возможно. Например, при измерении ускорения x(t) опорный сигнал Xr ограничен величиной земного тяготения g = 9,81 м.с2. Но измеряемое ускорение может достигать нескольких g, т.е. размах опорного сигнала в несколько раз меньше размаха измеряемого сигнала. На первый взгляд, невозможно аппроксимировать такой входной сигнал. Но уравнения оказываются умнее нас!
Численный пример 5.
Повторим Численный пример 1, но примем значения ступеней Xi опорного сигнала равномерно распределёнными между -0.1 и +0.1:
X1 = -0.1; X2 = -0.1/3; X3 = +0.1/3; X4 = +0.1.
Решением системы уравнений (12) получим следующие значения Ti:
T1 = -121.625×T; T2 = 395.250×T; T3 = -431.625×T; T4 = 159.000×T.
Значения T1 и T3 получились отрицательные. Это означает инверсное интегрирование. То есть если мы используем как интегратор счётчик импульсов, он должен работать на вычитание импульсов в течение времени T1 и T3. В случае аналогового интегратора, выходной сигнал датчика надо подавать на другой вход операционного усилителя. Действительно
| 4 | Ti | 4 | Ti | 4 | | | | |
| Wr = | S | òYi×dt = | S | ò(Xi + Xi3)×dt = | S(Xi + Xi3)×Ti = 14.5215 - 15.2936 - 17.4546 + 18.9767 = 3/4. | |
| i=1 | 0 | i=1 | 0 | i=1 | | | | |
Мы видим, что величина Wr равна величине Wr, найденной в Численном примере 1. Следовательно, и в этом случае погрешность измерения DV = 0.
Из выражения (14) мы видим, что величина Wr получается вычитанием "больших чисел" Yi×Ti. Это ограничивает чрезмерное сужение диапазона опорного сигнала Xr, ибо даже незначительная погрешность "большого числа" будет являться причиной большой погрешности конечной величины Wr. Поэтому надо по возможности расширять диапазон опорного сигнала, тем более что метод инвариантности позволяет, как видно из Численного примера 5, иметь значения ступеней опорного сигнала Xr за пределами входного сигнала x(t). Для случая интегрирования ускорения мы можем иметь диапазон опорнго сигнала Xr от -g до +g со всеми промежуточными значениями, что легко достигается поворотом акселерометра относительно местной вертикали.
Проиллюстрируем это Численным примером 6:
Повторим Численный пример 5, но опорные сигналы выберем только положительные, в диапазоне от 0 до 0.1: X1 = 0, X2 = 0.1/3, X3 = 0,2/3, X4 = 0.1. Тогда получим: T1 = -851.500×T, T2 = 2670.000×T, T3 = -2797.500×T, T4 = 980.000×T.
Как видим, инверсное интгрирование всё равно необходимо, а разброс "больших числен" увеличился, что снижает точность измерения.
3.8. Непрерывное измерение
До сих пор мы рассматривали однократное измерение, в одной точке траектории, в к-рой нам требовалось определить, когда скорость достигнет требуемого значения. В этой точке производится определённое действие, например, отделение ступени ракеты или её головной части. Но задание заранее значений ступеней опорного сигнала позволяет проводить измерение скорости непрерывно вдоль всей траектории.
Для этого ещё на земле проводится калибровка, определяющая значения ступеней опорного сигнала. Затем в полёте по нескольким измерениям в предыдущих точках троектории путём экстраполяции вычисляется ожидаемая скорость в следующей точке, и продолжительности ступеней опорного сигнала.
Определяются моменты ускорения в реальном полёте, а не ожидаемые по предыдущим испытаниям или теоретичским расчётам. Поэтому непрерывное измерение даёт весьма высокую точность.
4. Реализация метода инвариантности
Выше было описано применение метода инвариантности для пьезоэлектрического акселерометра, к-рым можно измерять ускорение, давление, вибрации и т.п.
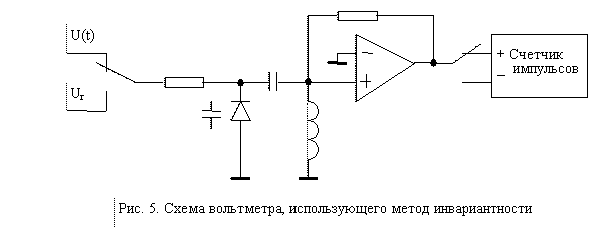
Возможно так же применение этого метода в вольтметре постоянного или переменного тока, построеннном на базе колебательного контура с варикапом, к к-рому приложено измеряемое напряжение (рис. 5). Изменение напряжения приводит к изменению ёмкости варикапа, и следоватльно к изменению частоты колебаний. Такой вольтметр обладает низким уровнем фликкер-шума (1/f шум), являющегося основной причиной погрешности вольтметра двухтактного интегрирования, а нелинейность его функции пробразования компенсируеся при помощи изложенного выше мтода инвариантности.
Литература
[1] Куликов С.В., Сибейкин С.С. Обеспечение инвариантности измерительно-вычислительных систем с помощью обобщённых критериев точности. - Вычислительная техника в автоматизированных системах контроля и управления. Межвузовский сборник научных трудов. Вып. 16. Пенза, Пензенский политехнический институт, 1986, с. 106-110.
[2] Куликов С.В., Сибейкин С.С. и др. Способ определения интегрального значения изменяющегося во времени измерительного сигнала. Авторское свидетельство СССР 1453418, 22 сентября 1988.
[3] Куликов С.В., Сибейкин С.С. и др. Устройство интегрирования изменяющегося во времени измерительного сигнала. Авторское свидтельство СССР 1544635Ю 8 октября 1989.
[4] Sergey Sergey Sibeykin. Method and device of determinftion of an input signal which changes in time. USA, Patent US No6240,435 bl, Date of Patent May 29, 2001.
[5] Ash, Robert B. Probability and Measure theory. 2000, pp. 174-176.
[6] Papoulis, A. Probability, Random Variables, and Stochastic Processes. 1965, pp. 88-103.
[7] Куликов С.В. Синтез и анализ импульсных измерительных преобразователей информационно-измерительных систем. М. Энергоиздат. 1982.
Вставка.
Можно непосредственно вычислить среднее значение измеряемой величины M[x] по значениям моментов показания
выходной величины y:
M1[x] = a1M1[y] + a2M2[y] + a3M3[y] + ;
здесь a1, a2, ... - коэффициенты разложения в ряд Маклорена функции x = f(y), обратной функции
преобразвания датчика y = f(x).
И вообще вычислить любой момент измеряемой величины x по следующей формуле:
Mn[x] = a1n-1{a1Mn[y]+na2Mn+1[y]+
na3Mn+2[y]+...} .
ЧАСТЬ II. ОТРИЦАТЕЛЬНЫЕ ВЕРОЯТНОСТИ
5.1. Отрицательным вероятностям посвящены ряд научных работ, включая статьи нобелевских лауреатов Поля Дирака [8] и Ричарда Фейнмана [9]. Однако всеобщего признания отрицательные вероятности не нашли, в основном по причине несоответствия с разработанной Колмогоровым [10] классической теорией вероятности: "Нет примера, по которому мы могли бы прямо определить отрицательные вероятности" [11]. Отрицательные вероятности встречаются, например, в квантовой механике, при применении столь экзотичного математического аппарата, как p-адические вероятности, причём даже здесь отношение к ним двойственное: "Хотя с математической точки зрения отрицательные вероятности бессмысленны*, имеется некоторый смысл в рассмотрении отрицательных вероятностей в физике" [12].
| * Положение спорное, ведь даже Фридрих Энгельс сморозил в "Диалектике природы" глупость о мнимых числах, утверждая, что они исчезают, едва лишь математик перестаёт думать о них. Энгельсу, не завершившему своего образования, простительно, ведь и Карл Маркс, окончивший и гимназию, и университет, уже в зрелом возрасте без особого успеха пытался постичь суть диффренциального исчисления. Об его тщетных потугах свидетельствуют дошедшие до нас "Математические рукописи Маркса". |
Встречаются отрицательные вероятности и в научно-популярной литературе, описывающей новейшие физические теории "для простаков". В [13] указано, что отрицательными вероятностями обладают такие экзотические и никогда не наблюдавшиеся элементарные частицы, как "духи", теоретически появляющиеся в современной "теории струн".
Я же столкнулся с отрицательными вероятностями при работе с выше-описанным методом инвариантности, где сигналы рассматривались как случайные величины, описываемые плотностью вероятности p(x).
Отрицательные плотности вероятности появлялись в случае, когда опорные сигналы Xi были существенно меньше измеряемого сигнала x(t). Тогда плотность вроятности p(Xr) опорного сигнала Xr может иметь как положительные, так и отрицательные значения, что соответствует прямому или инверсному интегрированию опорного сигнала.
Эти плотности вероятности p(Xr) характеризуют уже не просто опорный сигнал Xr, а тот, к-рый необходим для достижения минимальной погрешности конечного результата измерения - интеграла от измеряемого сигнала x(t).
Таким образом, не возникает противоречия с классической теорией вероятности, а отрицательные вероятности получают простую и наглядную интерпретацию.
Это стало возможным потому, что использовался один из введённых моим научным руководителем (рукой водителем, как любили говорить у нас на работе ))) С.В.Куликовым "обобщённых критериев точности" [7] - функционала, связывающего:
- погрешности измерительного преобразователя;
- плотность вероятности p(x) измеряемого сигнала x(t);
- алгоритм потребления информации - в нашем случае это интегрирование.
С.В.Куликов характеризовал плотность вероятности p(x) измеряемого сигнала x(t) при помощи ступенчатой аппроксимации [7]. Я же для этой цели (поскольку в то время институтский курс математики забыть ещё не успел ))) применил моменты случайных величин. Это и позволило добиться реальных результатов, а также попутно доказать полезность "обобщённых критериев точности*".
| * А вот как-то на одной научной конференции профессор Ш.Ю.Исмаилов, бывший научным руководителем моего Куликова, съязвил: "Обобщённые критерии точности, это, конечно, очень интересно, если они существуют" )). | | | |
5.2. Свойства отрицательных вероятностей и их интерпретация
Найдём плотность вероятности p(Xr) ступенчатого опорного сигнала Xr, покрывающего только часть входного сигнала x(t) и рассмотренного в Численном примере 3. Пусть Xmax = 10g и максимальные значения опорного сигнала равны -g и +g. Используя выражение (5), мы получим плотность вероятности p(Xr), изображённую на рис. 6. Значения d1 и d3 отрицательны, так как отрицательны значения T1 и T3.
Мы видим, свойство (3) плотности вероятности не выполнено, ибо часть её значений отрицательна. Зато свойство (4) выполняется, ибо
а интеграл от дельта-функции равен единице.
Знак "плюс" или "минус" значения плотности вероятности p(Xr) определяет, какое, прямое или инверсное, требуется интегрирование данной ступени опорного сигнала Xr. Следовательно, плотность вероятности p(Xr) описывает не только случайную переменную Xr, но и метод её преобразования. Назовём это "процессом преобразования". С.В.Куликов ввёл понятие "обобщённого критрия точности" как функционала, характеризующего, зависящей от погрешности измерительных преобразователей, плотности вероятности измерительного сигнала и алгоритма потребления информации [7]. Процесс преобразования является одним из таких обобщённых критериев точности, причём для него некоторые значения плотности вероятности могут быть отрицательны.

Рис. 6. Плотность вероятности p(Xr) ступенчатого опорного сигнала, подвергаемого
прямому и инверсному интегрированию, имет отрицательные значения. Моменты
M1, M2, M3 для p(Xr) и плотность вероятности p(x) одинаковы.
Отрицательные вероятности могут быть полезны при исследовании нелинейных систем, ибо здесь результаты прямого интегрирования положительной величины X и инверсное интегрирование отрицательной величины -X того же модуля не совпадают.
Заключение
Мы рассматривали входной x(t) и опорный Xr сигналы как случайные величины. Это позволило применять аппарат теории вероятности в теории измерений и получить новые результаты.
Если опорный сигнал Xr покрывает весь входной сигнал x(t), то плотность вероятности p(Xr) описывает только опорный сигнал Xr, мы получаем показание Wr опорного сигнала для скорости Vr.
Применение плотности вероятности, имеющих отрицательные значения, может быть полезно при исследовании нелинейных систем.
Литература
[8] Dirac P. The Physical Interpretation of Quantum Mechanics. 1942. Proc. Roe. Soc. London, (A 180), pp. 1-39.
[9] Feynman R.P. Negative Probability. 1987. Quantum Implications: Essays in Honour of David Bohm by F. David Peat(Ed.), Basil Hiley (Ec.), London and New York: Roytledge & Kegan Paul Ltd, nn/ 235-248.
[10] Колмогоров А.Н. Основные понятия теории вероятностей. М.: Наука, 1974.
[11] Espen Gaarder Haug. Derivatives Models on Models. 2007, pp. 317-333.
[12] Хренников А.Ю. Эксперимент ЭПР-Бома и неравенство Белла: квантовая физика и теория вероятностей. Теоретическая и математическая физика. Том 257б N 1, октябрь 2008. http://www.mathnet.ru/links/a392bf32452c41584b816026d8655/tmf6266pdf, стр. 105
[13] За пределами теории Эйтштейна - многомерные миры. Знание-сила, 10.03.2003. www.wilmott.com.
[14] Haug E.G. A Look in the Antimatter Mirror. Wilmott Magazine, 10.03.2003. www.wilmott.com.
[15] J. Sperling, W. Vogel. Representation of entanglement by negative quasi-probabilities. 2008. http://arxiv.org/abs/0811.4527.
[16] Holger F. Hofmann. How to simulate a quantum computer using negative probabilities. 2008. http://arxiv.org/0805.0029.
[17] Christopher Ferrie, Joseph Emerson. Frame representations of quantum mechanics and the necessity of negativity in quasi-probability representations. 2007.
[18] Slobodan Prvsnovic. The non-negativity of probabilities and the collapse of state. 2002. http://arxiv.org/abs/quant-ph/0211058.
[19] Thomas Curtright. Negative Probability and Uncertainty Relations. 2001. http://arxiv.org/abs/hep-th/0105226.
[20] Jose L. Cereceda. Local hidden-variable models and negative-probability measures. 2000. http://arxiv.org/abs/quant-ph/0010091.
[21] Hong-Chen Fu, Tyu Sasaki. Negative Binomial and Multinomial States: probability distribitions and coherent states. 1996. http://arxiv.org/abs/quant-ph/9610022.
ЧАСТЬ III. ОБОБЩЁННОЕ ОПРЕДЕЛЕНИЕ ИНТЕРВАЛА КОРРЕЛЯЦИИ
Abstract. Найдена сдедующая формула [22], обобщающая известные определения интервала корреляции tи:
| T | 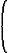 | | t
_
T | 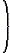 |
| tи = 2 | òr(t)× | 1- | ×dt |
| 0 |
где r(t) - нормированная корреляционная функция,
T - время измерения (интегрирования).
6.1. Суммирование случайных величин
Суммирование случайных величин с учётом корреляционных связей весьма сложно. Сравнительно просто суммировать лишь некоррелированные и жёстко-коррелированные случайные величины, для к-рых соответственно:
| DS = | SDi | | (19) |
| i |
| sS = | Ssi | | (20) |
| i |
| | __ |
| Здесь D - дисперсия, s = | Ö | D - среднее квадратическое отклонение |
Выражения (19) и (20) являются частными случаями общего выражения:
| | | | |
| DS = | SDi + 2ri,j× | S si×sj | | (21) |
| i | i<j | | |
где ri,j - корреляционный коэффициент между значениями погрешностей i и j.
Воспользоваться выражением (21) для вычисления результирующей погрешности, как правило, затруднительно, ибо неизвестны конкретные значения величин ri,j, и ведёт к слишко громоздким вычислениям.
Обычно пользуются следующим приёмом: погрешности, для к-рых корреляционный коэффициент ri,j ³0.7, полагают жёстко коррелированными, а для ri,j <0.7 - некоррелированными, после чего суммирование ведётся по формулам (19) и (20) [23].
Иными словами, интервал корреляции tи определяется значениями корреляционного коэффициента ri,j ³ 0.7.
6.2. Интервал корреляции и его извстные определения
В случае перехода от дискретных к непрерывным случайным величинам корреляционный коэфициент ri,j трансформируется в нормированную корреляционную функцю
r(t) = R(t)/D ,
гд R(t) - корреляционная функция (КФ) исследуемого случайного процесса, D = R(0) - его дисперсия.
Классическое определение интервала корреляции следующее - это длина наибольшего интервала времени, на к-ром корреляционная связь между значениями случайного процесса существенна для решаемой задачи [24]. Вот только как определить, когда корреляционны связи перестают быть существенными и становятся несущественными )).
Необходимы поэтому математические выражения для опрделения интервала корреляции tи. Их несколько:
В [25] приведено следующее выражение:
которым можно пользоваться, если p(t) не принимает отрицательных значений.
В случае исследования быстро затухающих колебательных процессов в [26] рекомендуется пользоваться выражением, в котором нормированная корреляционная функция берётся по модулю:
|
tи2 =
| 1
¾
2 | ¥ |
| òôr(t)ô×dt | | (23) |
| -¥ |
И, наконец, в [26] приведена следующая формула для определения интервала корреляции:
tи3 = | ¥ | | | (24) |
| òr(t)×t×dt |
| -¥ |
¾¾¾¾ |
| ¥ |
| òr(t)×dt |
| -¥ |
Все эти определения интервала корреляции не универсальны. Действитльно, ни одно из них не пригодно для вычисления, например, интервала корреляции гармонических незатухающих колебаний, где r(t) = cos Wt.
6.3. Интервал корреляции при применении операции интегрирования
Постараемся найти интервал корреляции tи в форме, пригодной при вычислении дисперсии результирующей случайных величин.
В основе определения интервала корреляции лежит аппроксимация нормированной корреляционной функции r(t) ступенчатой функцией, равной единице в пределах интервала корреляции и нулю за его пределами.
Пусть имеется случайный процсс V(t) и интеграл от него Q. Разобьём время интегрирования T на "n" циклов пррдолжительностью DТ. Тогда за время DT отклонение результата интегрирования DQ = V×DT и
Известно, что если случайный процесс Q является интегралом случайного процесса V(t), то их корреляционные функции RQ(t,t') и Rv(t,t') связаны следующим выражением [27]:
Rv(t,t') =
| d2RQ(t,t') | | (25) | |
| ¾¾¾¾ | | | |
| dt×dt' | | | |
Для решения поставленной задачи необходимо выбрать интервал корреляции tи таким, чтобы двойные интегралы в пределах от 0 до Т, взятые по dt и dt', от аппроксимирумой нормированной корреляционной функции и аппроксимирующей ступенчатой функции были равны.
Представим КФ, характеризующую случайный процесс отклонения результата интегрировани за цикл DQ как произведение соответствующих КФ, те.е как ироизведение их дисперсий и нормированных КФ R(t,t') = D[V]×r(t,t'). Тогда
| T | | | |
| D[Q] = D[V]× | òòr(t,t')dt×dt', | | (26) | |
| 0 | | | |
а дисперсия отклонения результата интегрирования за цикл:
| DT | | | |
| D[DQ] = D[V]× | òòr(t,t')dt×dt'. | | | |
| 0 | | | |
Величину D[V] из этого выражения подставим в формулу (26), из него найдём величину D[V] и подставим её в выражение (25). Тогда
| D[Q] = | | T | | (27) |
| D[DQ]× | òòr(t,t')dt×dt' | | | |
| 0 | | | |
¾¾¾¾¾¾¾¾ | | | |
| DT | | | |
| òòr(t,t')dt×dt' | | | |
| 0 | | | |
С другой стороны, суммируя вeличины DQ от цикла к циклу внутри интервала корреляции tи как жёстко-коррелированные, а за его прделами как некоррелированные, получим:
| D[Q] = D[DQ]×(tи/T)2×(T/tи). | | (28) | | |
Приравняв выражения (27) и (28), найдём искомый интервал корреляции:
| tи = | | × | T | | (29) |
| òò r(t,t')×dt×dt' |
| 4×DT2 | 0 |
¾¾¾ | ¾¾¾¾¾¾ | |
| T | 2DT |
| òò r(t,t')×dt×dt' |
| 0 |
Учитывая выражение (25) и то, что величины, выходящие за знак интеграла в числителе и знаменателе выражения (29) сократятся, после дву-кратного интегрирования получим:
| tи = | DT2 | r(T) + C1 + C2×T | | (30) |
¾¾ × | ¾¾¾¾¾¾¾¾¾, | |
| T | r(2DT) + C3 + 2×C4×T |
где C1, C2, C3, C4 - постоянные интегрирования.
В числителе выражения (30) написана первообразная функция для двойного интеграла в числителе выражения (29). Эта первообразная функция описывает дисперсию случайного процесса изменения величины DQ. При Т = 0 эта дисперсия равна нулю, и поскольку нормированная КФ r(0) = 1, то из выражения (30) следует, что при Т = 0 значение C1 = -1. Для стационарного случайного процесса DQ его дисперсияя ограничена какой-то постоянной величиной при T ® ¥, и тогда C2 = 0. Такое же рассуждение применимо и к знаменателю выражения (30). Тогда
| tи = | DT2 | × | 1 - r(T) | | (31) |
¾¾ | ¾¾¾¾¾ | |
| T | 1 - r(2×DT) |
Продолжим анализ интервала корреляции tи.
При T ® 0 нормированна КФ r(t,t') в знаменателе выражения (29) стремится к единице, и тогда знаменатель выражения (29) равен T3 и
| tи = | | T | | |
1
T | òò | r(t,t')×dt×dt'. | | (32) | |
| 0 | | | |
Вычислим полученный двойной интеграл, для чего введём новые переменные:
s = t' + t;
t = t' - t.
Произведём замену пременных, выразив величины t и t' через s и t:
t = (s - t)/2; t' = (s + t)/2.
Тогда
| a | | | | ¶(t×t')
---------
¶(s, t) | | | |
| tи = | 1
T | òò | r[t(s,t),t'(s,t)]× | ×ds×dt, | | (33) |
| | G | | |
где якобиан
¶(t×t')
---------
¶(s, t) | | 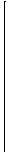 | ¶(t)
------
¶(s) | | ¶(t)
------
¶(t) |
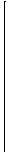 | = | 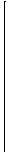 | 1/2 | | -1/2 | 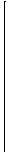 |
| = | | | | | | | = 1/2. |
| | ¶(t')
------
¶(s) | | ¶(t')
------
¶(t) | 1/2 | | 1/2 |
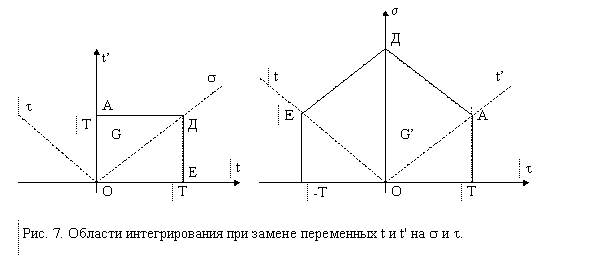
Область интегрирования G в координатах s и t принимает вид, изображённый на рис. 7 и ограничена прямыми ОА, ОЕ, АД и ДЕ, функции к-рых соответственно:
s = t, s = -t, s = 2T - t, s = 2T + t.
Следовательно
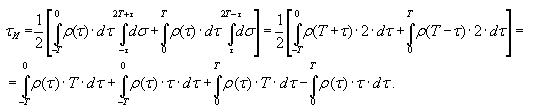
КФ всегда чётная, т.е. r(t) = r(-t), и тогда
| T | 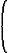 | | t
_
T | 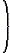 |
| tи = 2 | òr(t)× | 1- | ×dt | | (34) |
| 0 |
6.4. Оценка полученного результата
При T ® ¥ выражение (34) переходит в выражение (22) и, следовательно, является его обобщением. В то же время при выводе выражения (34) не требовалось соблюдать ограничения, заключающиеся в том, что нормированная КФ не должна принимать отрицательных значений. Следовательно, выражение (34) для tи обобщает выражение (22) для произвольной продолжительности измерения Т и случая отрицательных значений нормированной КФ. По этой же причине полученное выражение для для tи обобщает интервал корреляции, заданный выражением (23)
Найдём значения интервала корреляции tи для нескольких частных случаев нормированной корреляционной функции r(t).
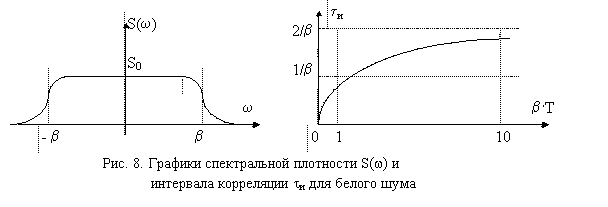
6.4.1. Белый шум
Спектральная плотность белого шума S0 постоянна в определённом диапазоне частот, обычно от 0 до некоторого значения b:
| S(w) = | __S0
_________ |
| 1 + (w/b)2 |
Она показана на рис. 8.
| | ¥ |
| Прибегнув к преобразованию Фурье R(t) = | 1
__
p | òS(w)×coswt×dw, найдём корреляционную |
| | 0 |
| | |
функцию белого шума. Она имеет вид экспоненты: R(t) =
| S0×b
____
_2 | |
×e-bôtô |
Соответствующая нормированная КФ r(t) = e-bô tô, и из выражения (34) находим интервал корреляции белого шума:
| tи = | 2
_
b | 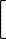 | 1 - |
1
___
b×T | (1 - e-
bT) | 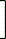 |
График этой зависимости приведён на рис. 8.
6.4.2. Гармонический процесс. Для него нормированная корреляционная функция r(t) = cos Wt. Тогда интервал корреляции в соответствии с формулой (34):
| tи = | 2
_____
W2×T | (1 - cosWT). |
Его график показан на рис. 9.
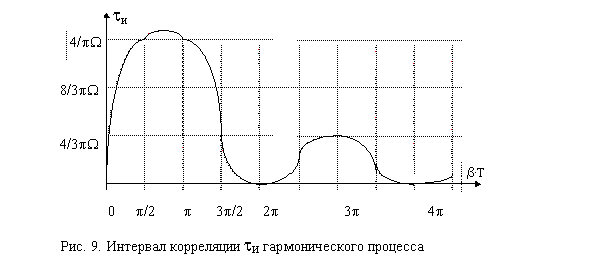
Из выражения (28) видно, что дисперсия D[Q] для r(t) = cosW×t будет равна нулю в момнты времени, кратные 2pWT. Действительно, как известно, для усреднения погрешности, вызванной периодической помехой, время измерения следует выбирать кратным периоду помехи.
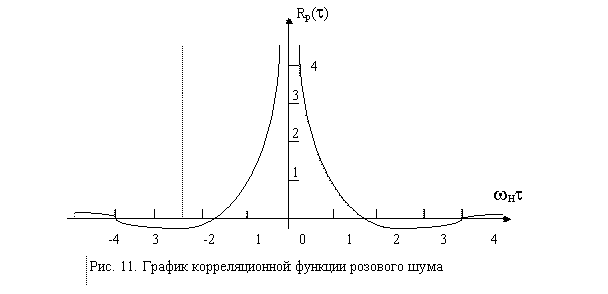
6.4.3. Розовый шум и его корреляционная функция.
Помимо белого и розового, есть ещё и зелёный шум*:
Идёт-гудёт зелёный шум,
Зелёный шум, весенний шум.
|
* По утверждению Н.А. Некрасова, зелёным шумом народ называет весеннее пробуждение природы - http://gold-stih.ru/?p=2056, но для нас это не болee чем поэтических образ )).
|
Розовый шум называют ещё фликкер-, низко-частотным, или 1/f шумом. Им характризуются самые разнообразные процессы - разливы Нила, шелест листьев, хороша музыка, всё это по спектру является розовым шумом. В связи с широким распространением в природе розового шума, человек хорошо адаптировался к нему, поэтому-то для нас комфортно всё, что соответствует ему по спектру.
Происхождение розового шума загадочно. Для объяснения его возникновения пытались привлечь даже такой экзотический математический аппарат, как дробные интегралы. Но сразу же возникает неизбежный вопрос: почему именно дробное интегрирование ответственно за возникновение розового шума? Вдаваться в вопросы происхождения розового шум мы не будем, а просто примем, что он дан нам самой природой.
Спектральная плотность розового шума носит гиперболический характер и на некоторой частоте w0 он переходит в блый шум. Композицию розового и белого шумов можно описать следующим выражением:
Sк(w) = S0 ×
| 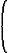 | w0
__
w |
+ 1
| 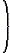 | | (35) |
А собственно розовый шум:
Интеграл от спектральной плотности S(w) по dw до ¥ даёт дисперсию и мощность. Для розового шума интегрирование в этих пределах даст бесконечность. Положим верхний предел равным w0, ибо тут начинается область белого шума. Но и при интегрировании от 0 до w0 мы получим бесконечность. Это, впрочем, естественно, ибо интегрирование от w = 0 означает, что время интегрирования Т®¥. Действительно, за миллиарды лет может произоёти всё что угодно. Но для реальной задачи время интегрировани Т огранично, и следовательно, нижним пределом интегрирования розового шума слдует положить некое значение wн = 1/T.
Вместе с тем нельзя пренебрегать и спектральной плотностью Sp(w) при w < wн. положим, что она в этом диапазоне w постоянна и гиперболична только при более высоких частотах w:
| S(w) = | S0×w0
_____
wн | , при w £ wн, |
и
S(w) = |
S0×w0
_____
w |
, при w ³ wн. |
Подвергнув эти выражения преобразованию Фурье, будем искать корреляционную функцию розового шума:
| 1
_
p | ¥ | S0w0
____
p | 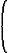 | wн | | | w | | | 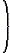 | | (37) |
| Rp = | òS(w)×coswt×dw = |
ò | coswt
_____
wн | ×dw + | ò | coswt
____
w | ×dw | |
| 0 | 0 | | | wн |
Второй интеграл в выражении (37) - это взятый с обратным знаком интегральный косинус Ci(wнt):
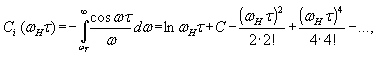 | | (38) |
где C = 0.5772... - постоянная Эйлера.
Примечание. Есть в математике 3 постоянные, к-рые всё время появляются в математических выражениях: это число p = 3.1415...*, основание натурального логарифма е = 2.718..., и постоянная Эйлера С = 0.5772... . Все эти три числа - иррациональные и трансцедентные, а вот почему они именно такие и почему всё время всплывают в различных математических формулах - никто не знает.
* Мнемоническое правило, приведённое Перельманом в "Занимательной математике" для запоминания числа p. Количество букв в каждом слове стихотворения равно цифре соответствующего разряда числа p:
Это я знаю и помню прекрасно,
Пи многие знаки мне лишни, напрасны.
И ведь правда - обычно мы пользуемся первыми двумя цифрами после запятой, и очень редко - четырьмя.
График интeгрального косинуса Ci(wнt) показан на рис. 10.
Разложив 1-й интеграл выражения (37) в ряд Маклорена и подставив в выражение (37) значение С из формулы (38), получим следующее выражение корреляционной функции розового шума.
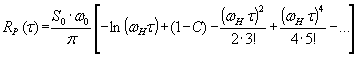 | | (39) |
Это выражение описыват всё ещё физически нереальный случайный процесс, ибо при t®0, Rp(t)®¥. Это естественно, ибо ограничение розового шума в области верхних частот не вводилось. Введём это ограничение, положив, что при t = 0 корреляционная функция Rp равна некоему постоянному значению, для чего введём в формулу (39) параметр a:
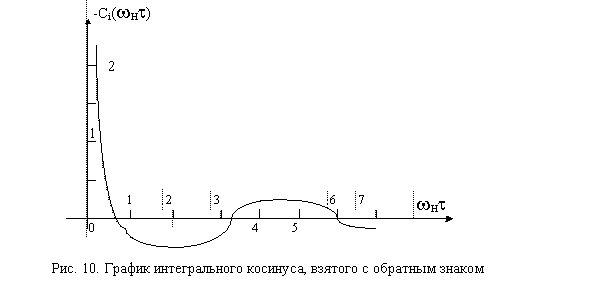 | | (39) |
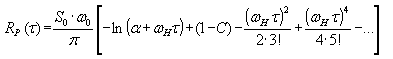 | | (40) |
Найдём диспрсию розового шума, проинтегрировав его спeктральную плотнось Sp(w), заданную выражением (35), в диапазоне частот от 0 до w0, при к-рой розовый шум переходит в высокочастотный белый шум. Получим:
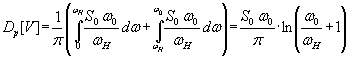 | | (41) |
С другой стороны, из выражения (40) следует:
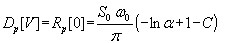 | | (42) |
Сравним выражения (41) и (42), найдём значение a:
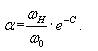 | | (43) |
График корреляционной функции розового шума прдставлен на рис. 11.
6.4.4. Интегрирование розового шума
Имеем случайный процесс V(t), характеризуемый корреляционной функцией Rv(t,t'), и интеграл от него: Q(t) = òV(t)×dt. Найдём дисперсию D[Q] результата интегрирования.
Для этого можно воспользоваться выражнием (26):
| T |
| D[Q] = D[V]× | òòp(t,t')dtòdt'. |
| 0 |
Вычисляя двойной интеграл так же как мы это делали в пункте 6.3, и учитывая, что корреляционная функция всегда чётная r(t = r(-t, получим:
| T | 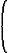 | | t
_
T | 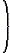 | | (44) |
| D[Q] - 2×D[V]×T× | òr(t)× | 1- |
| 0 |
В этой формуле легко просматриваетсяя выведенное нами ранее выражение (34) для корреляционной функции
| T | 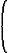 | | t
_
T | 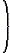 |
| tи = 2 | òr(t)× | 1- | ×dt |
| 0 |
Следовательно, выражение (44) принимает следующий вид:
D[Q] = D[V]×tи×T,
Умножив и разделив это выражение на tи, получим:
| T
__
tи |
| D[Q] = D[V]×tи2× | , | | (45) |
Видим, что эта формула соответствует сложению погрешностей, жёстко коррелированных на интервале t и и некоррелированных за его пределами
Теперь подставим в выражение (44) корреляционную функцию розового шума, полученного в соответствии с формулой (40). После вычислений мы получим:
| 2×S0×w0
______
p |
D[Q] =
|
×T2
| | (46) |
Из выражения (46) следует, что при розовом шуме увеличение времени измерения Т не позволяет снизить погрешность измерения. Это является основной причиной, не позволяющей добиться дальнейшего повышения точности вольтметра двойного интегрирования. Такой же результат ещё ранее был получен в [29]. Понятно, почему человек чувствует себя комфортно при розовом шуме - он избавляет нас от излишних подробностей, от излишка информации, отягощающей нашу память и органы чувств )).
В то же время, сравнивая выражени (45) и (46), нетрудно видеть, что для розового шума интервал корреляции формально равен времени измерения.
И на этом я заканчиваю изложение своей творческой деятельности в области измерений.
Литература
[22] Сибейкин С.С. Разработка и исследование интегрирующих частотно-цифровых преобразователей с коррекцией аддитивной помехи. Авторефрат диссертации на соискание учёной степени кандидата технических наук. ДСП. М.: 1987.
[23] Новицкий П.В. Основы информационной теории измерительных устройство. - М.: Энергия, 1968.
[24] ГОСТ 21878-76. Случайные процессы и динамически системы. Термины и определения. - М.: Изд-во Стандартом. 1976.
[25] Харкевич А.А. Борьба с помехами. - М.: Наука, 1964.
[26] Тихонов В.И. Статистическая радиотехника. - М.: Св. радио, 1966.
[27] Вентцель Е.С. Тория вероятностей. М.: Наука, 1964.
[28] В.А.Бесекерский, Е.П.Попов. Теория систем автоматического регулирования. М.: Наука, 1966.
[29] Малиновский В.Н. Основы теории и проектирования цифровых измерительных приборов с высокими метрологическими характеристиками. Авторефрат диссертации на соискание учёной степени доктора технических наук. М.: 1976.
ДОПОЛНЕНИЕ. АППРОКСИМАЦИЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Не всегда необхдимо аппроксимирвать входной сигнал ступенчатой функцией, ступени которой в вероятностном смысле отображаются дельта-функциями.
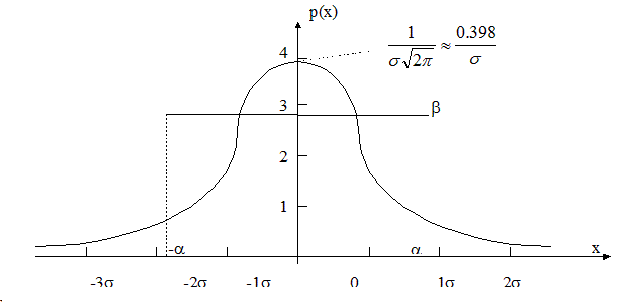
1. Давайте аппроксимируем плотность вероятности цнтрированного нормального распределения
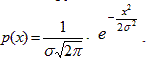
В качестве аппроксимирующей функции выберем равномерное распределение pr(x).
pr(x) = b, если - a < x < a
pr(x) = 0, если x < - a или x > a.
Поскольку математические ожидания равны нулю, будем искать величины a и b из условий равенства 0-го и 2-го моментов плотностей вероятностей p(x) и pr(x), что эквивалентно равенству площадей под кривыми плотностей вероятностей (которые всегда равны 1) и их дисперсий. Дисперсия равномерного распределения
| a | a | 2
__
3 | |
| D = | òp(x)x2dx = | òbx2dx = | ba3 | |
| -a | -a | | |
Следовательно, имеем систему уравнений
| 1 = 2ab; | 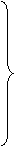 |
| s2 = | 2
__
3 | ba3 |
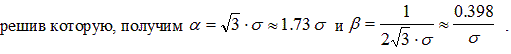
| ¥ |
| 2. В [30] аналогичная задача аппроксимации решалась из условий равенства энтропий - | òp(x)ln[p(x)]dx. |
| -¥ |
Было получено, что эквивалентный интервал неопределённости dэкв = 2a » 2.07 s.
3. Найдём также аппроксимацию методом наименьших квадратов. Численным методом (file c:\\tp7\tp\bin\approc.fas) было найдено, что минимум квадратической погрешности аппроксимации будет при a» 1.54. Квадратичная погрешность при этом около 19%.
[30] Электрические измерения неэлектрических величин, под ред. П.В.Новицкого. Энергия, 1975.
На первую страницу сайта